prof. dr. sc. Vesna Županović
Fraktalna svojstva bifurkacija dinamičkih sustava – FRABDYN
| Šifra projekta: PZS-2019-02-3055 |
| Ustanova: Sveučilište u Zagrebu, Fakultet elektrotehnike i računarstva |
| Suvoditelj projekta: prof. dr. sc. Pavao Mardešić, Université de Bourgogne, Dijon (Francuska) |
| Trajanje projekta: 1.10.2019. – 31.5.2023. |
| Web stranica projekta |
Područje našeg istraživanja vezano je uz kvalitativnu teoriju dinamičkih sustava, teoriju singularnih perturbacija, fraktalnu geometriju, kompleksnu analizu i numeričko modeliranje dinamičkih sustava. Kvalitativna teorija diferencijalnih jednadžbi i dinamičkih sustava proučava rješenja jednadžbi bez eksplicitnog rješavanja jednadžbi, jer to nije moguće za velike klase diferencijalnih jednadžbi koje su važne u raznim granama znanosti i inženjerskoj primjeni. Ponašanje sustava modelira se diferencijalnom jednadžbom ili diskretnim dinamičkim sustavom, ovisno o tome možemo li promatrati vrijeme kontinuirano ili diskretno s nekim korakom. Diferencijalne jednadžbe generiraju dinamičke sustave s kontinuiranim vremenom, a rekurzivne jednadžbe generiraju diskretne dinamičke sustave. Često se za proučavanje nekog fenomena kombiniraju oba pristupa, jer postoje prednosti jednog i drugog. Kad nešto mjerimo ili računamo nekim softwareom, imamo diskretne podatke, ali matematički je lakše raditi s kontinuiranim sustavima.
Jednadžbe koje proučavamo prirodno ovise o parametrima, stoga dodavanjem parametra u dinamički sustav dolazimo do teorije bifurkacija, gdje bifurkacija znači kvalitativnu promjenu ponašanja sustava. Sustav koji prolazi kroz bifurkaciju može promijeniti stabilnost, što je ključni problem u matematičkom modeliranju. Teorija singularnih perturbacija proučava rješenja diferencijalnih jednadžbi s obzirom na parametar 𝛿 → 0, gdje se rješenja pri 𝛿 = 0 drastično razlikuju od graničnih rješenja pri 𝛿 → 0. Teoriju singularnih perturbacija u 1990-ima značajno su razvili profesori Freddy Dumortier sa Sveučilišta u Hasseltu, i Robert Roussarie s Université de Bourgogne. Član našeg tima docent Renato Huzak, hrvatski istraživač iz belgijske grupe sa Sveučilišta u Hasseltu, bivši je doktorand i suradnik F. Dumortiera i P. De Maesschalcka.
Granični ciklusi, izolirane periodične orbite, mogu se roditi u bifurkacijama sustava, kao i u singularnim perturbacijama sustava. Slavni neriješeni 16. Hilbertov problem traži gornju ogradu za broj graničnih ciklusa polinomijalnog vektorskog polja stupnja određenog stupnja. Suvoditelj projekta profesor Pavao Mardešić, ugledni istraživač iz hrvatske dijaspore i naslovni redoviti profesor na Prirodoslovno-matematičkom fakultetu u Zagrebu, dobio je važne rezultate u smjeru 16. Hilbertovog problema.
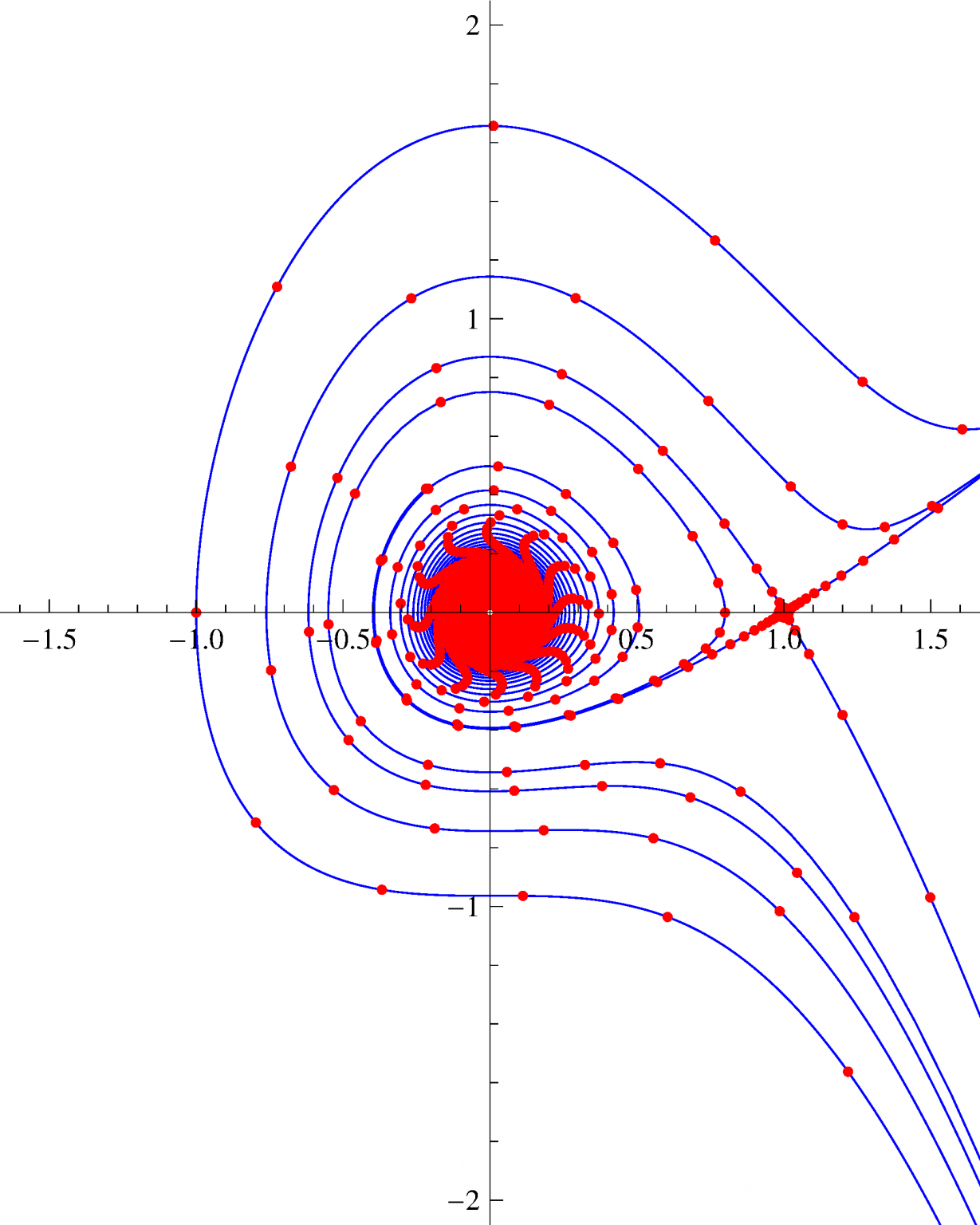
U projektu FRABDYN se na spomenute probleme primjenjuju ideje povezane s fraktalnom geometrijom koje su prvi put objavljene u članku D. Žubrinić, V. Županović, Fractal analysis of spiral trajectories of some planar vector fields. // Bulletin des sciences mathématiques. 129 (2005) 6; 457-485. Taj pristup je posebnost naše grupe te daje izvrsne nove rezultate kad se spaja s već poznatim teorijama. Ideja je da se svojstva dinamičkog sustava mogu očitati iz površine ili duljine (općenito mjere) ε-okoline orbite sustava. Tu površinu u pravilu ne možemo izračunati točno, već računamo asimpotski razvoj i temeljem članova asimptotskog razvoja izvodimo neke zaključke o ponašanju sustava. Fraktalne dimenzije koriste se da bi se kvantitativno opisali komplicirani objekti, kao što su klasični fraktali-Kochova pahuljica, trokut Sierpinskoga i slični, te za neobične atraktore kao na primjer Lorenzov ili Henonov. Fraktalna dimenzija za razliku od topološke ne mora biti cijeli broj. Intuitivno, kad vidimo objekt kao što je Kochova pahuljica, lako možemo prihvatiti ideju da to nije obična krivulja, te da joj je dimenzija veća od 1, ali ipak manja ili jednaka 2 jer leži u ravnini. Ima različitih fraktalnih dimanzija, ali mi koristimo box dimenziju jer je prikladna za klasifikaciju objekata koji imaju akumulaciju samo oko nekih točaka ili krivulja, a ne „posvuda” kao Kochova pahuljica. Ti objekti koje mi proučavamo su orbite dinamičkih sustava. Box dimenzija se očitava iz vodećeg člana asimptotskog razvoja, ali i drugi članovi razvoja daju važne informacije o sustavu. U sustave se uključuju parametri, te se na taj način proučavaju bifurkacije, što je potpuno novi pristup.
Grupa pod vodstvom profesora M.L. Lapidusa s University of California Riverside proučava fraktalne zeta funkcije. Njegovi suradnici, među kojima je i član našeg tima, docent Goran Radunović, doktorand M. L. Lapidusa i D. Žubrinića, koriste kompleksnu analizu i Mellinovu transformaciju kao glavne alate za konstrukciju fraktalnih zeta funkcija ε-okoline orbita, te za proučavanje zeta funkcija s obzirom na parametre. Štoviše, fraktalne zeta funkcije su povezane s poznatom Riemannovom zeta funkcijom.
U ovom projektu su već dobiveni izvrsni rezultati spajanjem spomenutih teorija s idejom hrvatske grupe. Određeni rezultati su i numerički verificirani korištenjem Wolframove Mathematice i algoritama razvijenih unutar ovog projekta, te se rad na tome nastavlja. Član istraživačke grupe FRABDYN projekta doc. dr. sc. Domagoj Vlah, zajedno s kolegom s Instituta za fiziku dr. sc. Tomislavom Ivekom osvojio je prvu nagradu na natjecanju Data Challenge u okviru konferencije Extreme Value Analysis Conference (EVA 2021). Algoritmi korišteni na ovom natjecanju povezani su s algoritmima koji se razvijaju u okviru projekta.
Doktorand Vlatko Crnković radi iz područja singularnih perturbacija i fraktalne geometrije pod mentorstvom Renata Huzaka i Domagoja Vlaha. Poslijedoktorand Martin Klimeš radi na analizi bifurkacija pomoću Lapidusove teorije zeta funkcija i integralnih transformacija, kao što su Mellinova, Laplaceova i Borelova. Klimeš već ima veliko iskustvo iz područja analitičke klasifikacije sustava pomoću Borelove i Laplaceove transformacije.
Dodatne informacije o projektu možete poslušati u gostovanje voditeljice projekta u emisiji Hrvatskog radija Znanstveni koncentrat 7. lipnja 2021. godine.

Vesna Županović rođena je 1965. godine u Splitu. Obrazovala se u Zagrebu, pri čemu je 1979. upisala XV. gimnaziju, nakon toga studij matematike na PMF-u u Zagrebu, gdje je diplomirala 1988., magistrirala 1992., a doktorirala 1997. pod mentorstvom Pavla Mardešića. Nakon diplome kratko radi u XV. gimnaziji, a nakon toga se u studenom 1988. zapošljava kao asistentica na Zavodu za primijenjenu matematiku FER-a, gdje sada radi na mjestu redovite profesorice u trajnom zvanju. Od 2008.-2012. bila je predstojnica Zavoda. Znanstveni interes su joj dinamički sustavi i fraktalna geometrija, pri čemu su članci objavljeni u vrhunskim časopisima, kao na primjer četiri članka u Journal of Differential Equations, koji je tijekom godina na listi SCIE-Mathematics u 5-10% najboljih časopisa, te članak u Advances in Mathematics 2016. Ističe se i pozvani članak u Encyclopedia of Mathematical Physics, Elsevier 2008. Pod njezinim voditeljstvom obranjene su 3 doktorske disertacije. Osim znanstvenih projekata, angažirana je i na stručnim i popularizacijskim projektima. Dobitnica je Državne nagrade Faust Vrančić za 2019., a od svibnja 2021. je predsjednica Hrvatskog matematičkog društva.


